· LEY DE POISEUILLE.
Se define viscosidad a la resistencia opuesta por los fluidos al movimiento en alguna de sus partes. Por el fenómeno de la viscosidad, la velocidad de los fluidos por los tubos crece de las paredes al centro del tubo, ya que en los puntos pegados a la pared, el fluido se adhiere a ella frenándose por su viscosidad. Por efecto de esta viscosidad, hay una perdida de carga a lo largo del tubo.
Por esto a la formula de Bernuilli hay que sumarle un termino referido a la perdida de carga y que se denota por hf representando la perdida de carga por frotamiento.
Hay diferentes ecuaciones que tiene en cuenta la variable viscosidad como son las ecuaciones de Navier. Gracias a su expresión se puede obtener la llamada ley de Poiseuille: “el caudal de fluido por un tubo cilíndrico en régimen laminar, es directamente proporcional a la cuarta potencia del radio, R, y a la diferencia de presiones entre la parte superior del tubo e inferior p, e inversamente proporcional a la longitud de este, l, y al coeficiente de viscosidad del líquido,
Consideremos ahora un fluido viscoso que circula en régimen laminar por una tubería de radio interior R, y de longitud L, bajo la acción de una fuerza debida a la diferencia de presión existente en los extremos del tubo.
F=(p1-p2)p r2
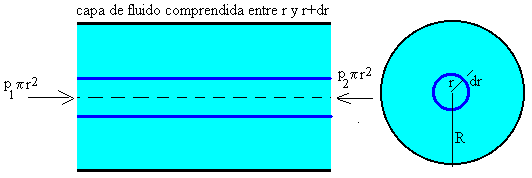
Sustituyendo F en la fórmula (1) y teniendo en cuenta que el área A de la capa es ahora el área lateral de un cilindro de longitud L y radio r.
El signo negativo se debe a que v disminuye al aumentar r.
· Perfil de velocidades
Integrando esta ecuación, obtenemos el perfil de velocidades en función de la distancia radial, al eje del tubo. Se ha de tener en cuenta que la velocidad en las paredes del tubo r=R es nula.